
The resulting function is known as a composite function.

Let us assume we know the domains of the functions f and g separately. The process of combining functions so that the output of one function becomes the input of another is known as a composition of functions. All Modalities Composition of Functions Loading. Function composition is only one way to combine existing functions. Also included in this set are worksheets on evaluating the compositions of two functions. It is important to know when we can apply a composite function and when we cannot, that is, to know the domain of a function such as f\circ g. Composition of Functions ( Read ) Algebra CK-12 Foundation Composition of Functions The output (range) of one function becomes the input (domain) of another. Featuring two levels of exercises on finding the composition of two functions, they reiterate that composition of functions f(g(x)) means combining the functions where the output of one g(x) becomes the input of the other f(x). You should see =8 in the bottom right corner.Īs we discussed previously, the domain of a composite function such as f\circ g is dependent on the domain of g and the domain of f. In the next line enter h\left(f\left(2\right)\right). Enter the functions above into a graphing calculator as they are defined. You can check your work with an online graphing tool. The table below shows the composite functions f\circ g and g\circ f as tables. Then, using the table for g, we can evaluate Second of all, even if g(x) is defined, it has to be in the domain of f. First off, the x has to be in the domain of g if g(x) were say 1/x, then x 0 could not be in the composite domain.
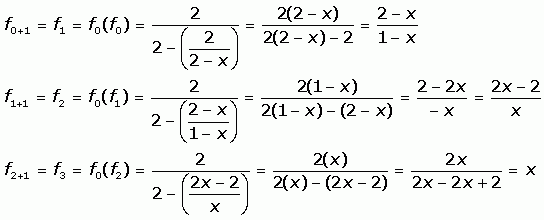
To evaluate g\left(f\left(3\right)\right), we first evaluate the inside expression f\left(3\right) using the first table: f\left(3\right)=3. The domain of a composite function f(g(x)) is all x in the domain of g such that g(x) is in the domain of f. The function T\left(d\right) gives the average daily temperature on day d of the year. The key idea in function composition is that the input of the function is not a numerical value, instead, the input is also another function. The function C\left(T\right) gives the cost C of heating a house for a given average daily temperature in T degrees Celsius. Composite Functions The Organic Chemistry Tutor 5.87M subscribers Join Subscribe 27K Share Save 1.9M views 5 years ago New Precalculus Video Playlist This algebra video tutorial provides a basic. defines contours γ = γ( c n, z) that follow the flow of the vector field f( z).Using descriptive variables, we can notate these two functions. There are several notations describing infinite compositions, including the following:įorward compositions: F k, n ( z ) = f k ∘ f k + 1 ∘ ⋯ ∘ f n − 1 ∘ f n ( z ). For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.Īlthough the title of this article specifies analytic functions, there are results for more general functions of a complex variable as well. For infinite compositions of a single function see Iterated function. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. How do you find the domain for the composition of two functions, latexfcirc. If the order is reversed when composing two functions, can the result ever be the same as the answer in the original order of the composition If yes, give an example. We will do this with specific numerical inputs for functions expressed as tables, graphs, and formulas and with variables as inputs to functions expressed as formulas. What is the composition of two functions, latexfcirc g/latex 3.

Mathematically speaking, the range (the y -values) of one function becomes the domain. So, basically, a function is applied to the result of another function. The term ' composition of functions ' (or ' composite function ') refers to the combining together of two or more functions in a manner where the output from one function becomes the input for the next function. It means here function g is applied to the function of x. Once we compose a new function from two existing functions, we need to be able to evaluate it for any input in its domain. In Maths, the composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h(x) g(f(x)). Some functions can actually be expanded directly as infinite compositions. Evaluate a composition of functions using an equation. In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Mathematical theory about infinitely iterated function composition


 0 kommentar(er)
0 kommentar(er)
